
(page 1000(2))

|
(page 1000(2)) |
|
| Proof By Induction | |||||||||||||||||
There is a very useful way of proving things about the positive
numbers called induction.
It works this way.
Let's say I have an idea about the natural numbers,
for example:
Moves for Towers of Hanoi of size N is 2N - 1
We'll represent this idea for number n as Idea(n).
To prove Idea(n) works for all numbers n greater than or equal to 1 we take 3 steps:
How does this prove Idea(n) is true for all n? Well if it's true for 1, then let the k in step II be 1. Then, provided we did step III correctly, then it's true for k+1, which is 2. If it's true for 2, it's true for 3, which means it's true for 4, and so on for as high as you'd like to go.
Proving Our Idea is Correct |
For this discussion Moves(N) means the number of moves
needed to solve a Towers of Hanoi puzzle of N rings.
So we are trying to prove that:
| Moves(N) = 2N - 1
Step I |
Moves(1) is 1, and 21 - 1 is also 1, so Idea(1) is true.
| Step II |
Assume that Idea(k) is true for some k.
| Step III |
Using our recursive algorithm on
page 100(2), we can move a tower of
size k+1 from A to B by
performing the following steps:
|
Therefore adding the moves take by the three steps we get: Moves(k+1) = Moves(k) + 1 + Moves(k) Given our assumption made in Step II and substituting in our idea, we get: Moves(k+1) = (2k - 1) + 1 + (2k - 1) = 2k + 2k - 1 + 1 - 1 = 2 × 2k - 1But what is 2 × 2k? It's 2 × (2 × 2 ... k times), which is 2 × 2 ... k+1 times) which is 2k+1. Therefore: Moves(k+1) = 2k+1 - 1which is what we wanted to prove. | |||||||||
| hanoi08.qh - 1.6 - 05/10/02 |
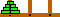
|