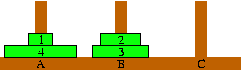
(page 111(2))
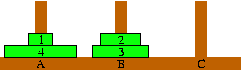
|
(page 111(2)) |
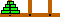
|
| How Many Moves Does it Take? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Before we can answer that we need to explore the powers of 2.
| The Powers of 2 |
The powers of 2 are the series of numbers you create when you
multiply 2 by itself numerous times as in:
| 2 × 2 = 4 2 × 2 × 2 = 8 2 × 2 × 2 × 2 = 16and so on. These are very important numbers. They are used in computers and in all sorts of other ways. They are very useful in a variety of games and puzzles, including the Towers of Hanoi. But once we start to multiply 2 by itself lots of times, it gets tedious to write all those 2 × 2 × ... so we have a notation (a way of writing) a power of 2. 2 × 2 × ... (N times) = 2NHere is a table of the powers of 2 up to N:
Now Back to Hanoi |
Now let us compare the powers of 2 to the number of moves for the
various tower sizes by putting them in a table together.
|
Looking at the table, it would appear that the number of moves required to solve a Towers of Hanoi puzzle of N rings is 2N - 1. At least that formula works for 1, 2, 3, 4, 5, and 6. It would also appear that 20 would be 1, but we'll get back to that later. In the meantime, is there a way to prove that our 2N - 1 works for all values of N? | ||||||||||||||||||||||||||||||||||||||||||||||||||
| hanoi07.qh - 1.6 - 05/10/03 |
|