Towers of Hanoi Adventure

The Towers of Hanoi and Adventures in Mathematics
(page 100(2))

The Towers of Hanoi Solution
	Did you see the pattern that was developed in the previous page? Basically if we wanted to move a tower of size N (where N is a natural number greater than zero) from A to B, we: Move tower of size N minus 1 from A to C; Move the N-ring from A to B; Move tower of size N minus 1 from C to B. and if N is zero, we do nothing. So to move a tower of size N from A to B: If N is greater than zero then Move tower of size N minus 1 from A to C; Move the N-ring from A to B; Move tower of size N minus 1 from C to B.
Recursion
	The above instructions, or algorithm, is what we call recursive -- it calls itself. It is said to involve recursion. Those dictionary definitions weren't much help were they? Basically a recursive procedure, is one that invokes itself to solve a smaller version of the problem in order to solve the bigger problem. So in the Towers of Hanoi puzzle for a tower of size N, we use recursion to move towers of size N - 1, and as we recurse the N gets smaller until it reaches zero, which is trivial to solve. Neat isn't it? Recursion is a very important concept and is used a lot in computer programs.

hanoi04.qh - 1.4 - 05/10/02
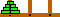