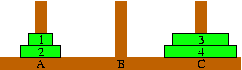
(page 1101(2))
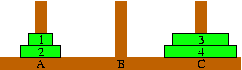
|
(page 1101(2)) |
|
| Binary Numbers | |||||||||||||||||||||||||||||||
|
Binary numbers are just like decimal numbers, just using a
different base, namely 2 rather than 10.
Let's convert the decimal number 85 to a binary number. We'll need the table of the 2 power series.
Rumour has it that one reason MicroSoft got interested in 64 bit words is that Bill Gates (the principal owner of MicroSoft and the richest person in the world) wanted to be able to fit his net worth into a word, as 4 Billion just wasn't big enough. To convert 85 we'll subtract the highest possible powers of 2 until we reach zero, recording the results: 85 - 64 = 21 21 - 16 = 5 5 - 4 = 1 1 - 1 = 0 So: 85 = 64 + 16 + 4 + 1 85 = 26 + 24 + 22 + 20 85 = 1×26 + 1×24 + 1×22 + 1×20 85 = 1×26 + 0×25 + 1×24 + 0×23 + 1×22 + 0×21 + 1×20 The addition of the 0×2N terms into the above addition is to what Prof. Arsham was referring in the quotation on page Page 1011(2). If we remove the remove the `×2N' and plus signs we get: 85(10) = 1010101(2) The zeros are required to keep the 1s in the correct place. You might have noticed the page numbers at the top of the page and have recognized that these are binary numbers. But have you noticed the relationships between these numbers and the Towers of Hanoi that is running in the top left hand corner? It turns out that the number can be used to determine the ring to be moved. Look at the binary page number and find the first `1' starting from the right hand end. If the first 1 is in the first position from the right, or the 20 position, then ring 1 is moved. If first 1 is in the second position, ring 2 is moved, and so on. The odd numbered rings move left to right, as in A to B to C to A. The even numbered rings move right to left, as in A to C to B to A. | |||||||||||||||||||||||||||||||
| hanoi13.qh - 1.5 - 05/10/03 |
|