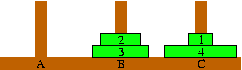
(page 1010(2))
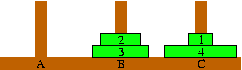
|
(page 1010(2)) |
|
| So How Many Moves Will the Monks Have to Make? | |||||||||||||||||||||||
So we now know that the number of moves required to complete
a Towers of Hanoi puzzle of N rings is 2 N - 1, the monks who are
working on a tower of 64 rings are going to take:
2 64 - 1which equals: 18,446,744,073,709,551,615
So What About a Tower of Size 0 |
Does our formula hold for a tower for size 0?
Obviously it takes 0 moves to move a tower of 0 rings,
so:
| 2 0 - 1 = Moves(0) = 0 2 0 - 1 = 0 2 0 = 1But let's look at that another way:
So what is 2 -1? By continuing the series, 2 -1 is 2 0/2 which is 1/2. Therefore 2 -1 is ½. Similarly 2 -2 is 1 / (2 2) which is ¼. In fact we can state that 2 -N is 1/ (2 N) and 1 / (2 M) is 2 -M. If we want to multiply powers we just add the exponents as in: 2 3 × 2 4 = 2 3 + 4 This also makes it easy to divide a power by a power. 2 N ÷ 2 M = 2 N × 2 -M = 2 N-M | |||||||||||||||||||||
| hanoi10.qh - 1.4 - 05/10/02 |
|