(page 11(2))
|
|
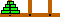
(page 11(2)) |
|
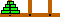
| Solving the Towers of Hanoi | |
|
Did you get stuck? If you were using the computer game,
were you able you do it in the least possible number of moves?
So starting with:
Well if you could move a tower of size 3 from A to B, as in:
Well that seems to work, but how do you move a tower of size 3
from A to B. Well you move a tower of size 2 from A to C as in:
But this still depends on moving a tower of size 2 from A to C, so how do you do that. Well you move a tower of size 1 from A to B, moves the 2-ring to C, and then move the tower of size 1 from B to C. But how do you move a tower of size 1 from A to B. Just as you did above, you move a tower of size 0 from A to C, move the 1-ring from A to B and then move the tower of size 0 from C to A. And how do you move a tower of size 0? There's nothing to it ;) Why did I bother with the tower of size 1 nonsense? Obviously one could immediately move the 1-ring and not bother thinking about towers of size 1. It turns out that thinking about towers of size 1, makes it easier to talk about the solution, which we will continue on the next page. |
| hanoi03.qh - 1.3 - 05/10/02 |
|
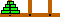
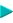
how do you solve the problem of moving a tower of size 4 from A to C?
, then you could move the 4-ring to C
giving: 
.
Finally you could move the tower of size 3 from B to C
giving: 
.
and then move the 3-ring
from A to B 
and then move the tower of size 2 from C to B,
giving