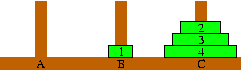
(page 1111(2))

|
(page 1111(2)) |
|
| So How Long Will the Monks Take? | |||||||||
|
Let's assume the monks are making a move every second.
How many moves is that a year?
There are approximately 365 and a quarter days in an average year, 24 hours in a day, 60 minutes in an hour, and 60 seconds in a minute so that makes: 365.25 × 24 × 60 × 60 = 31,557,600 seconds in a year Dividing the number of moves the monks have to make by the number of moves per year: 18,446,744,073,709,551,615 ÷ 31,557,600 = 584,542,046,090.62639That's more than 584 billion years, or 5.8E11 years. We probably have time to get a sandwich.
Doing Big Number Calculations |
I have a program on my system that can operate on huge numbers,
but most are limited to 32 or 64 bit numbers, so performing the
above division may be difficult.
Given that we don't really need the precision (to 5 decimal places
no less), one could resort to do the calculation with scientific
notation, in which case it's a lot easier.
The above division becomes:
| 1.8E19 ÷ 3.1E7 = 1.8/3.1 × 1019-7 = 0.58E12 = 5.8E11
What if the Monks Computerized? |
But what if the monks built a incredibly fast robot that could do
a billion moves a second?
| With our understanding of powers of 10, we can divide 5.8E11 by 1E9 which gives us 5.8E2 -- more than half a millennium. So this is getting a little nearer, and our great20 grandchildren may have to worry. But is this possible? If the monks could build such a machine, let's try to watch the 1 ring as it is moved. Well we can't. It's moving way too fast. If the needles are a metre apart, the 1-ring would move a metre every 2 billionth of a second, or 5E8 metres per second. Given that the speed of light is 2.99E8 metres per second, the 1-ring would be moving at about 1.67 times the speed of light, which Einstein said is impossible, so I guess we don't have to worry much. | |||||
| hanoi15.qh - 1.8 - 05/10/03 |
|